Sinusoidal Functions Review

There are a number of ways to approach the sinusoidal/periodic function. We were taught to use either GRAPHMATICA or a graphing calculator.


The periodic function equation is y=Asin(Bx+C)+D and that is what you will input into the software of your choice.

A=Amplitude
B=Period (formula for period P=2(pi)/B)
C=Phase shift
D=Verticle shift

Here is a site that demonstrates those values (very usefefull to play around with it)-http://www.ronblond.com/M12/sc.APPLET/index.html

If you are given the sinusoidal function(periodic function) and want to graph it using a calculator
1. press[mode] and make sure that it is on radian NOT degrees
2. press [y=] and input the formula Asin(Bx+C)+D (substitue numbers)
3. press [graph] and behold the squiggly lines
-you may want to adjust the windows setting to get a better picture

If the information is given in tabular data then you will have to use something called SinReg
1. press [stat] and put the data into a list
2. press [stat]-> calc then go down to something called SinReg
3. back at the home screen put in SinReg,L1,L2,Y1
4. turn on the stat plot ([2nd y=]) and press graph

And that my friends is periodic functions in a nut shell.

Sequences and Series Review

Ok, this is a little late. I would use slideshare for this but, it doesn't want to work nicely. I'll just give you a download link while I fix slideshare.

Sequences and Series PPT

(Sept 10/09)
Update: The PPT link actually works out pretty well and if I were to change the Show to be nice with Slideshare I would have to change quite a bit. I'm just going to leave it the way it is.

Here's the Standard Deviation unit, in a nutshell. Click on the images below and there's typing explaining them that you can't see just by viewing them.

OK guys were going to work with Vectors. Now it's pretty easy... A Vector is anything with a direction and a magnitude. First thing to do is draw a rough looking diagram just to show you more less what is going to look like and to make sure that your on the right track.



Some key words and phrases are:

One of the things you going to run into is a ''Bearing" a bearing will be given to you in a number, that number is the amount of degrees it is clockwise from north. For example a bearing of 90 would mean that it would straight east.

If you know your directions your going to get this...



These are the few different directions that your going to end up getting....

North of East
East of North
East of South
South of East
South of West
West of South
West of North
North of West

For example if you have "North of East" you would look at the north spot and travel East. Now to throw something else in there is going to be a number like "North 45 East"

Always start with the first direction you are given and go clockwise or counter clockwise in the amount of degrease you are given.

When your writing your question down you have to be as accurate as possible because you will be given two or more directions and have to measure the distance back...

This is Vector addition

As you see the first direction it is done as i said but the second direction is a bit more tricky. When you draw you first line just draw it till the distance you need to go. For example it may say 5km when of coarse you couldn't draw it. Make a scale that makes since to the amount of space you have to draw it. 1km may be one centimeter. When you draw your second line you must imagine or draw a norther grid as the end of line and draw the second line just like the first.


If the question asks you what is the distance, "the way the crow flys" it's as simple as measuring the distance back to the staring point. If you have drawn it to scale and wrote down the right distances just use a ruler for the distance.

Good luck...

Stats unit review, (confidence intervals)

This is a piece of the STATS unit review.
Confidence intervals.

A confidence interval is… “Predicting the likelihood that the mean of a sample occurs within a certain interval, a certain percent of the time”.

90%...95%...99%... sizes of confidence intervals considered “worthwhile” for statistical prediction purpose.

Here is an example question:
A research study on fruit flies found that an average of 50% of them stay alive after 32 hours.

a) Determine the 95% confidence interval for the percentage of a sample of 1000 fruit flies still alive after 32 hours. Show your work.
Here is what you do.

In your calculator, press the buttons… STAT then TESTS. Go to Prop z-int and it brings up this screen.
X:
N:
C-Level:
Calculate

X is your mean, N is your total number, so in this example your X would be 500, and your N would be 1000. Your C-level is 95. Press calculate and you should get this screen.
1-PropZInt
(.046901,.053099)
P=.5
N=1000

Your percentage interval is (.046901,.053099)
After every question you need to explain the meaning of the confidence interval. So in this example you would write….

If a similar experience/survey/poll were conducted this interval (46.9, 53.1) means that we are 95% confident that 32 hours later out of the 1000 fruit flies between 46,9 and 53.1 percent of them will remain alive.

I hope you are confident with this part of the unit, and if you have any questions please place them in the comments section and I will do my best to answer them.

Grouped Data

We learnt about grouping data, and ways to use use it.Grouped Data is data put into a chart or organized as a group.

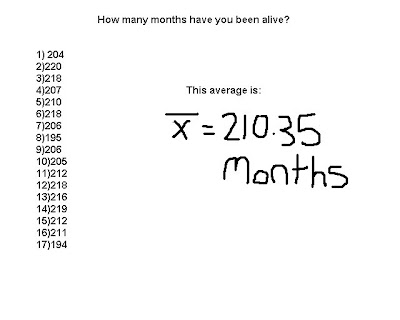As a class we did an example:You find the average by adding up all your results from the data and divide by how many sets there are. In our example we took the sum of everything and divided by 17 to get 210.35 as an average.
There are many ways of organising data (T-chart, Venn Diagram, Etc)
Here is another way of showing our results:

Here we took the averages, and used tally marks to show how many of the numbers from our data fall into place of the averages. Your tally marks must add up to how many sets of numbers you have. In our Example our tally marks add up to 17.

Probability

Sample Space -can be defined as any complete and total representation of the outcomes in a probabaility situation.

Ex. Roll a regular 6 sided die; spin a spinner (numbered 1-4).

Represent/show/display/sketch…. “The sample space”
6x4=24 possible out comes in the sample space.

The sample space is:
(1, Green) (1, Red) (1, Orange) (1, Blue)
(2, Green) (2, Red) (2, Orange) (2, Blue)
(3, Green) (3, Red) (3, Orange) (3, Blue)
(4, Green) (4, Red) (4, Orange) (4, Blue)
(5, Green) (5, Red) (5, Orange) (5, Blue)
(6, Green) (6, Red) (6, Orange) (6, Blue)

Everything and al possibilities are displayed

Mutually Exclusive and Mutually Inclusive Events

mutually exclusive events CANNOT occur together

ex:

Events A and B are mututally exclusive, they are disjoint sets. ( they have no common members)

The following formula is the only formula to be used with mutually exclusive events ONLY!

P(A or B)= P(A) + P(B)

ex: What is the probability in a regular deck, on a single card flip, of drawing a face card or a 5?

A: face card

B: 5

P(A or B)= P(A)+P(B)
P(f or 5)=P(f)+P(5)

=12/52+4/52
=16/52
=4/13 or 31%

Mutually inclusive events DO happen together

ex:

A:face card- 12/52
B: red cards-26/52

38/52 is WRONG

because you cannot count them twice!!

the correct way to do this is:

P(AorB)=P(a)+P(B)-P(A and B)

=12/52+26/52-6/5

=32/52 or 8/13 or 61.5%'

*use venn diagrams* put examples of mutually inclusive and exclusive events venn diagrams

the above are venn diagrams of the two examples given earlier.
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
INDEPENDENT/DEPENDENT EVENTS
*involves chronology of events(order in time)

Independent events do NOT have an effect on each other (ie. successive coin flips)these events are random.

Dependent events do have an impact on some subsequent probability event (ie. newest thing Depends on an older thing) these are not random.

example of dependent events

ex: "with or without replacement"
socks from a drawer
balls from an urn
Take for example the famous game off of "The Price Is Right" 3-Strikes game.

Fundamental Counting Principle:

When order doesn’t matter you use nCr. You enter the first number (number of letters in the alphabet, number of 5 cards poker hands, etc…), press math, PBR, nCr, the second number (the number of letter code words/the number of diamonds and hearts, etc…).

When order does matter you use nPr. You enter the first number (number of letters in the alphabet, number of 5 cards poker hands, etc…), press math, PBR, nPr, the second number (the number of letter code words/the number of diamonds and hearts, etc…).

Compliments:
A'=(1-A)
A+A'=1

The definition of A is one thing or one sample. The definition of A' is everything else involved except A.

Pascal's Triangle:

Starting at the house CO-OP you head home but have to stop at Bob’s house to pick up your homework. You can only head South and East. How many ways can you get home from the CO-OP while stopping at Bob’s house?

Imagine encountering a problem like this…DON’T RUN AWAY IT’S EASY!!
You use Pascal’s Triangle. You first figure out the larger rectangle then the square.

You start off by adding the two ones to get 2. You then add the next one on the side and the two you just got to get three, you continue by adding the two numbers beside each other and putting their sum in the box below UNTIL you reach the red square, this is the stop point. You then start again in the new square and stop at the stop point.
You then add the two numbers that are in the red boxes, which are 126 and 6.
126+6=132

So therefore there are 132 ways to get from CO-OP to Home.

Design and Measurement

For our class assignment my group is in charge of Design and Measurement so hear it is.

In the Design and Measurement unit every thing was pretty straight forward. Basically all that you had to do was multiply the amount of material that you were using and multiply it by the price of the material, or if your looking for how much material there is left over you subtract how much you use by the total material used. Vice versa if your looking for how much material you used.

Here is an example.

A ballpark is to be built according to the following diagram.

A fence is to be put up around the entire park.

Fencing costs $1.35 per running foot.

The infield area that is to have shale on it needs to be dug down 18"(inches) so that one foot of gravel can be put down as a base and the 6"(inches) of shale put on top.

The cost of excavation is $9.00 per cubic yard.

Gravel costs $7.00 per cubic yard and shale costs $9.50 per cubic yard.

The remaining area of the park needs to have 4"(inches) of topsoil on it and sod put on top of the soil.

Topsoil costs $20 per cubic yard and sod costs $1.25 per square foot.

The grass needs to have fertilizer as soon as it is laid.

The fertilizer costs $15.60 per bag and a bag will cover 75 square yards.

Find the total cost of this project.

P.S.T. at 7% and G.S.T. at 5% apply to all materials used. Only G.S.T. applies to the excavation cost.

Start off by finding the area of the entire park, the infield and outfield, this will save you some time later on.

Area of entire ballpark is Area=Pi r^2 (Pi radius squared)

     =Pi 240^2

     =180955.7 /4 = 45238.9 feet square

Area or infield is Area=Pi r^2 (Pi radius squared)

      =Pi 125^2

      =49238.4 /4 = 12271.85 feet square

You have to divide these two answers by 4 because you are finding the area of an entire circle and you only want the area of a quarter the entire circle.

To find the outfield area subtract the infield are from the entire ballpark area.

45238.9 - 12271.85 = 32967.05 feet square

Now we can start figuring out the cost of the park.

Cost of Fence- Perimeter = 2Pi r

     = 2Pi 240

     = 1508 /4 = 377 + 2(240) = 857 * $1.35 = $1156.95

Cost of infield

Excavation- Cost = 1.5 * 12271.85 /27 = 681.8 * $9.00 = $6136

When finding the cost of something that is in yards we need to divide by 27 because the area we found is in feet.

Cost of Shale- Cost = 1/2 foot or .5 * 12271.85 = 227.3 * $9.50 = $2159.35

Cost of Gravel- Cost = (1 foot or 1 * 12271.85) /27 = 454.51 * $7 = $3181.57

Cost of Topsoil- Cost = (4 inches/12 inches * 32967.10) /27 = 407 * $20 = $8140

Cost of Sod- Cost = 32967.10 * $1.25 = $41208.88

Cost of Fertilizer- Cost = 32967.10 /27 /75 = 16.3 * $15.60 = $254.30

Now add up all of the purple prices to get a total of $56101.05

Now find the total excavation cost tax included. $6136 * 1.05 = $6442.8

Then find the total material cost plus tax. $56101.05 * 1.12 = $62833.18

Finally add the two totals in red to get your final total of $69275.98

today we did some math stuff. we learned about half-life and maintenance level. half-life is half the time for half the substance to be gone. maintenance level is when a person ingests a substance at regular time intervals, the amount of the substance in the blood eventually levels off, of stabilizes.

using microsoft excel for sequences

today in class we used a program called microsoft Excel. it was an easier way to find out the answer for sequences in a faster manner. you type in the first couple formulas and titles and from your specific question. ex. =b2*2 or =C2+.5. then scroll to the bottom to find the answer for the specific number your looking for.

today we learned about sequences
sequences are very exciting and fun to do
there are 2 different kinds of sequences
arithmatic sequences are found by adding or subtracting a common number ex: 2,4,6,8
geometric sequences are found by multiplying a common ratio
ex: 2,4,8,16
a recursive formula is based on the preceding term
the formula is tn=tn-1x2
nMin=1st term
u(n)=formula
u(mim)=value of first term
on the calculator

intro to sequences

The lesson today was too big for EDLINE, so I posted it here.