Sample Space -can be defined as any complete and total representation of the outcomes in a probabaility situation.
Ex. Roll a regular 6 sided die; spin a spinner (numbered 1-4).
Represent/show/display/sketch…. “The sample space”
6x4=24 possible out comes in the sample space.
The sample space is:
(1, Green) (1, Red) (1, Orange) (1, Blue)
(2, Green) (2, Red) (2, Orange) (2, Blue)
(3, Green) (3, Red) (3, Orange) (3, Blue)
(4, Green) (4, Red) (4, Orange) (4, Blue)
(5, Green) (5, Red) (5, Orange) (5, Blue)
(6, Green) (6, Red) (6, Orange) (6, Blue)
Everything and al possibilities are displayed
Mutually Exclusive and Mutually Inclusive Events
mutually exclusive events CANNOT occur together
ex:
Events A and B are mututally exclusive, they are disjoint sets. ( they have no common members)
The following formula is the only formula to be used with mutually exclusive events ONLY!
P(A or B)= P(A) + P(B)
ex: What is the probability in a regular deck, on a single card flip, of drawing a face card or a 5?
A: face card
B: 5
P(A or B)= P(A)+P(B)
P(f or 5)=P(f)+P(5)
=12/52+4/52
=16/52
=4/13 or 31%
Mutually inclusive events DO happen together
ex:
A:face card- 12/52
B: red cards-26/52
38/52 is WRONG
because you cannot count them twice!!
the correct way to do this is:
P(AorB)=P(a)+P(B)-P(A and B)
=12/52+26/52-6/5
=32/52 or 8/13 or 61.5%'
*use venn diagrams* put examples of mutually inclusive and exclusive events venn diagrams
the above are venn diagrams of the two examples given earlier.
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
INDEPENDENT/DEPENDENT EVENTS
*involves chronology of events(order in time)
Independent events do NOT have an effect on each other (ie. successive coin flips)these events are random.
Dependent events do have an impact on some subsequent probability event (ie. newest thing Depends on an older thing) these are not random.
example of dependent events
ex: "with or without replacement"
socks from a drawer
balls from an urn
Take for example the famous game off of "The Price Is Right" 3-Strikes game.
Fundamental Counting Principle:
When order doesn’t matter you use nCr. You enter the first number (number of letters in the alphabet, number of 5 cards poker hands, etc…), press math, PBR, nCr, the second number (the number of letter code words/the number of diamonds and hearts, etc…).
When order does matter you use nPr. You enter the first number (number of letters in the alphabet, number of 5 cards poker hands, etc…), press math, PBR, nPr, the second number (the number of letter code words/the number of diamonds and hearts, etc…).
Compliments:
A'=(1-A)
A+A'=1
The definition of A is one thing or one sample. The definition of A' is everything else involved except A.
Pascal's Triangle:
Starting at the house CO-OP you head home but have to stop at Bob’s house to pick up your homework. You can only head South and East. How many ways can you get home from the CO-OP while stopping at Bob’s house?
Imagine encountering a problem like this…DON’T RUN AWAY IT’S EASY!!
You use Pascal’s Triangle. You first figure out the larger rectangle then the square.
You start off by adding the two ones to get 2. You then add the next one on the side and the two you just got to get three, you continue by adding the two numbers beside each other and putting their sum in the box below UNTIL you reach the red square, this is the stop point. You then start again in the new square and stop at the stop point.
You then add the two numbers that are in the red boxes, which are 126 and 6.
126+6=132
So therefore there are 132 ways to get from CO-OP to Home.
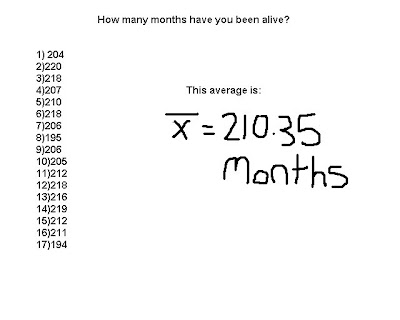You find the average by adding up all your results from the data and divide by how many sets there are. In our example we took the sum of everything and divided by 17 to get 210.35 as an average.
